Lehrinhalte
We will discuss the structure of lattices and lattice points in polyhedra, and their relation to discrete optimization from a geometric point of view.
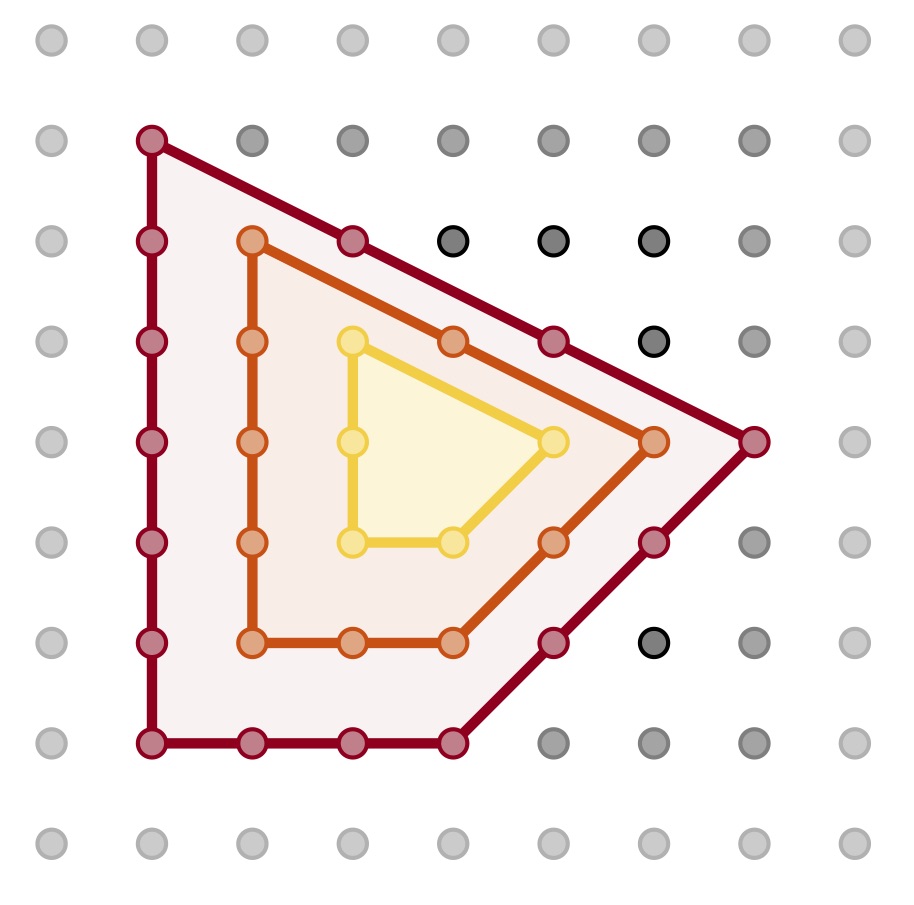
Lattices are the set of integer linear combinations of a set of linearly independent vectors in some (finite dimensional) vector space. An important and well known example is the lattice Z[sup]n[/sup] of integer points. The feasibility question in integer optimization asks whether a given polyhedron contains a point of this lattice.
The starting point in this lecture is the geometry of numbers. The fundamental theorems in this field consider conditions under which a convex body contains a point of the lattice. This area of research started with Minkowski's First Theorem stating that any centrally symmetric convex body of large enough volume contains an integer point. The algorithmic approach to this ask to find a lattice point in a polyhedron, if such a point exists. While this problem is known to be NP-complete in general, we will see that there is a polynomial time algorithm if the dimension is fixed. This is based on the computation of short vectors in lattices and the flatness theorem, which gives a universal bound (depending on the dimension) to the width of convex bodies without lattice points in the interior. We will also address the problem of counting lattice points in polyhedra, both from a geometric and algorithmic viewpoint. This will lead us to Ehrhart theory and, on the algorithmic side, to the polynomial time counting algorithm of Barvinok (again in fixed dimension).
Topics of the course will include
[list]
[*]Lattices and Polyhedra
[*]Geometry of Numbers, Minkowskis and Blichfeldts theorems
[*]Lattice basis reduction and the LLL-algorithm
[*]the shortest vector problem
[*]integer programming in fixed dimension via Lenstra's algorithm
[*]Rational generating functions and Barvinoks counting algorithm
[/list]
If time permits we may the shortly consider integer points in parametric polyhedra or cuts and lattice free polytopes.
Literature
Dimitris Bertsimas und Robert Weismantel, Optimization over Integers, Dynamic Ideas, (2005).
Rekha Thomas, Lectures in geometric combinatorics, AMS (2005).
Alexander Barvinok, A Course in Convexity, AMS (2002)
Jesus De Loera, Raymond Hemmecke, Matthias Köppe, Algebraic and Geometric Ideas in the Theory of Discrete Optimization, SIAM (2012)
Voraussetzungen
recommended: Introduction to Optimization, preferably also Discrete Optimization
Online-Angebote
moodle
We will discuss the structure of lattices and lattice points in polyhedra, and their relation to discrete optimization from a geometric point of view.
Lattices are the set of integer linear combinations of a set of linearly independent vectors in some (finite dimensional) vector space. An important and well known example is the lattice Z[sup]n[/sup] of integer points. The feasibility question in integer optimization asks whether a given polyhedron contains a point of this lattice.
The starting point in this lecture is the geometry of numbers. The fundamental theorems in this field consider conditions under which a convex body contains a point of the lattice. This area of research started with Minkowski's First Theorem stating that any centrally symmetric convex body of large enough volume contains an integer point. The algorithmic approach to this ask to find a lattice point in a polyhedron, if such a point exists. While this problem is known to be NP-complete in general, we will see that there is a polynomial time algorithm if the dimension is fixed. This is based on the computation of short vectors in lattices and the flatness theorem, which gives a universal bound (depending on the dimension) to the width of convex bodies without lattice points in the interior. We will also address the problem of counting lattice points in polyhedra, both from a geometric and algorithmic viewpoint. This will lead us to Ehrhart theory and, on the algorithmic side, to the polynomial time counting algorithm of Barvinok (again in fixed dimension).
Topics of the course will include
[list]
[*]Lattices and Polyhedra
[*]Geometry of Numbers, Minkowskis and Blichfeldts theorems
[*]Lattice basis reduction and the LLL-algorithm
[*]the shortest vector problem
[*]integer programming in fixed dimension via Lenstra's algorithm
[*]Rational generating functions and Barvinoks counting algorithm
[/list]
If time permits we may the shortly consider integer points in parametric polyhedra or cuts and lattice free polytopes.
Literature
Dimitris Bertsimas und Robert Weismantel, Optimization over Integers, Dynamic Ideas, (2005).
Rekha Thomas, Lectures in geometric combinatorics, AMS (2005).
Alexander Barvinok, A Course in Convexity, AMS (2002)
Jesus De Loera, Raymond Hemmecke, Matthias Köppe, Algebraic and Geometric Ideas in the Theory of Discrete Optimization, SIAM (2012)
Voraussetzungen
recommended: Introduction to Optimization, preferably also Discrete Optimization
Online-Angebote
moodle
- Lecturer: Andreas Paffenholz
Semester: ST 2022
Jupyterhub API Server: https://tu-jupyter-t.ca.hrz.tu-darmstadt.de